Rainbow set

Given sets $P_1, \dots, P_m$
$P = \{e_1, \dots, e_n\}$ is rainbow
if $e_i \in P_{\sigma(i)}$ and $\sigma(i)$'s are distinct

Example: 3 matchings of size 3

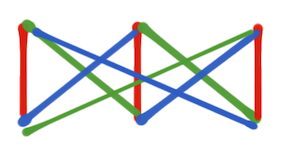
Rainbow matching of size 3

Rainbow matchings are
matchings in one dimension higher

Latin square

Conjecture (Ryser 1967) Every Latin square of odd order has one transversal.

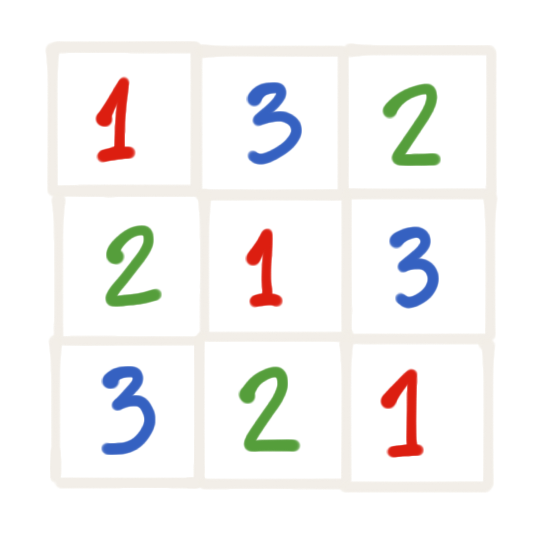
Equivalently If $n$ is odd and edge set of $K_{n,n}$ is decomposed into prefect matchings $E_1, \dots, E_n$ then there is a rainbow perfect matching

Pokrovskiy: $n$ matchings of size $n+o(n)$ in a bipartite graph have a rainbow matching of size $n$.

Woolbright: $n$ matchings of size $n$ in a bipartite graph have a rainbow matching of size $n - \sqrt{n}$.

Drisko: $2n-1$ perfect matchings in $K_{n,n}$ have a rainbow perfect matching.

Drisko's theorem: $2n-1$ (sharp) perfect matchings in $K_{n,n}$ have a rainbow perfect matching.

Drisko and Erdős–Ginzburg–Ziv

Drisko's theorem $2n-1$ perfect matchings in $K_{n,n}$ have a rainbow perfect matching.

EGZ Theorem Given $2n-1$ numbers in $\mathbb{Z}/n \mathbb{Z}$
there exist $n$ of them that sum to $0$.

Alon's proof of EGZ

For each number $a_i$, let $E_i$ be matching $\{ x \sim x + a_i\}$
By Drisko's theorem, there is a rainbow matching
$$1 \sim 1 + a_{i_1}, \dots, n \sim n + a_{i_n}$$$$\implies 1 + \dots + n = (1 + a_{i_1}) + \dots + (n + a_{i_n})$$

Plan of talk

Geometric proof of Drisko

Generalizations of Drisko

Topological proof of "fractional" Drisko

Bárány's colorful Carathéodory theorem

Carathéodory's theorem (cone version):
If $x \in \mathbb{R}^d$ lies in cone $\{\sum c_ip_i : c_i \ge 0, p_i \in P\}$ of $P$
then $x =$ the cone combination of $\le d$ points in $P$.

Bárány's theorem (cone version):
If $x \in \mathbb{R}^d$ lies in $\mathrm{cone}(P_i)$ for $i\in[d]$
then $x$ lies in the cone of a rainbow set.

Geometric proof of Drisko

edge set $E_i$ $\Leftrightarrow$ point set $P_i := \big\{\vec{e}_{ij} : i\sim j \text{ in }E_i\big\}$
$E_i$ is perfect matching $\implies$ $\vec{1} \in \mathrm{cone}(P_i)$
Fix: $P_i$ and $\vec{1}$ live in a 1-codimensional subspace of $\mathbb{R}^{2n}$
Bárány's theorem says $\vec{1}$ is in the cone of a rainbow set
$\Leftrightarrow$ fractional matching number $\nu^*($rainbow set$)=n$
Fact: $\nu^*$ = $\nu$ in bipartite graphs

Plan of talk

Geometric proof of Drisko

Generalizations of Drisko

Topological proof of "fractional" Drisko

Not necessarily perfect matchings

Theorem (Aharoni and Berger) $2n-1$ bipartite matchings of size $n$ have a rainbow matching of size $n$.

Geometric proof fails due to arbitrarily large dimension

Theorem (Aharoni, Kotlar and Ziv) $2n-1$ bipartite matchings of size $1,2,\dots,n,n,n,\dots, n$ have a rainbow matching of size $n$.

Hypergraph generalization

Theorem (Aharoni, Holzman, J.)
Given $r\in\mathbb{N}$, $n\in\mathbb{N}$ and $r$-partite edge sets
$E_1, \dots, E_{rn-r+1}$ with $\nu^*(E_i) \ge n$
there is a rainbow set $E$ with $\nu^*(E) \ge n$.

Here $\nu^*(E) = \max_f\sum_{e\in E} f(e)$
s.t. $f(e)\ge 0$ for $e\in E$ and $\sum_{e\ni v} f(e) \le 1$ for $v\in V$.

Plan of talk

Geometric proof of Drisko

Generalizations of Drisko

Topological proof of "fractional" Drisko

Simplicial complex $\mathcal{C}$ is a family of sets such that $\sigma \subseteq \tau, \tau \in \mathcal{C} \implies \sigma\in \mathcal{C}$.

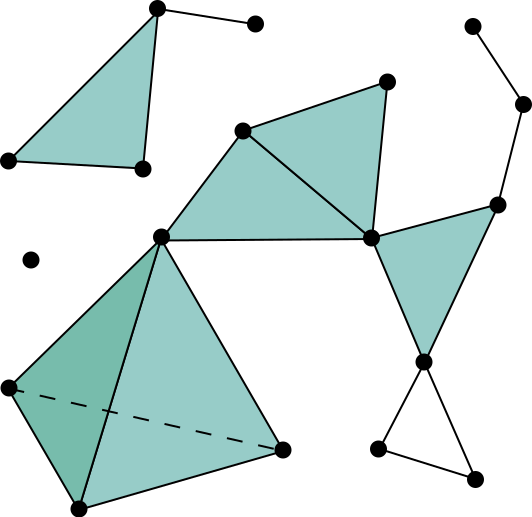
Theorem (Kalai–Meshulam)
Given $d\in\mathbb{N}$, $d$-Leray simplicial complex $\mathcal{C}$
matroid $M$ with rank function $\rho$, both on ground set $X$
If $\rho(X\setminus \sigma) > d$ for every $\sigma \in \mathcal{C}$, then $M\setminus \mathcal{C}\neq \emptyset$.

Theorem (Kalai–Meshulam)
Given $d\in\mathbb{N}$, $d$-Leray simplicial complex $\mathcal{C}$
matroid $M$ with rank function $\rho$, both on ground set $X$
If $\rho(X\setminus \sigma) > d$ for every $\sigma \in \mathcal{C}$, then $M\setminus \mathcal{C}\neq \emptyset$.

Application Given $E_1, \dots, E_{2n-1}$ with $\nu^*(E_i) \ge n$
$d = 2n-2$, $X = \cup E_i$, $\mathcal{C} = \{E \subseteq X : \nu^*(E) < n\}$
$M = \{\text{rainbow sets}\}$, $\rho(E) = \#$ of $E_i$ s.t. $E\cap E_i\neq\emptyset$
Cheated! $M$ not a matroid; can be fixed.
Kalai–Meshulam: $\exists E\in M\setminus\mathcal{C}$ assuming $\mathcal{C}$ is $d$-Leray

How to prove $\mathcal{C}$ is $d$-Leray?

Theorem (Wegner)

Elementary $d$-collapse

1. Pick $\sigma \in \mathcal{C}$ s.t. $|\sigma|\le d$ & max face $\tau \supseteq \sigma$ is unique;
2. Remove $[\sigma, \tau]$ from $\mathcal{C}$

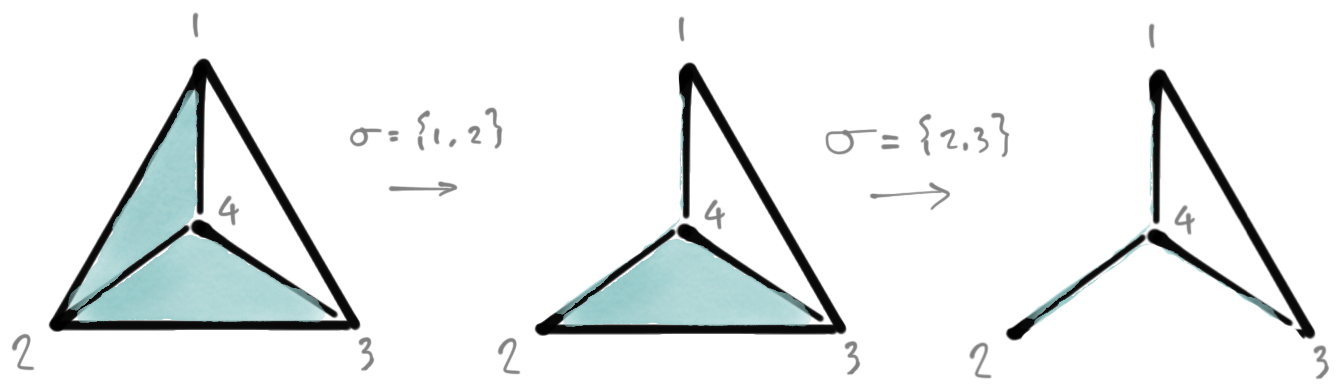
$\mathcal{C}$ is $d$-collapsible if $\mathcal{C}$ becomes $\{\emptyset\}$
through a chain of elementary $d$-collapsings

Variation and open problems

Not neccessarily $r$-partite

Theorem (Aharoni, Holzman, J.)
Given $r\in\mathbb{N}$ and $m\in\mathbb{R}^+$.
For $r$-edge sets $E_1, \dots, E_{\lceil rm\rceil}$ with $\nu^*(E_i) \ge m$
there is a rainbow set $E$ with $\nu^*(E) \ge m$.

Conjecture $2n$ (sharp) matchings (not necessarily bipartite) of size $n$ have a rainbow matching of size $n$.

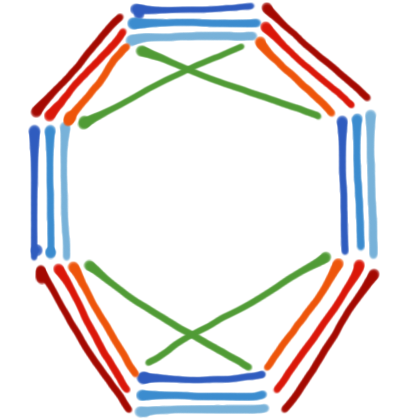
Theorem (Aharoni, Berger, Chudnovsky, Howard, Seymour) $3n-2$ matchings of size $n$ have a rainbow matching of size $n$.