Rainbow phenomena
| 1 | 3 | 2 |
| 2 | 1 | 3 |
| 3 | 2 | 1 |
Ryser's conjecture
Every Latin square of odd order has one transversal.
Rainbow reformulation
If an $n$ by $n$ (odd) complete bipartite graph is decomposed into $n$ perfect mathings, then there exists a rainbow perfect matching.
Caccetta–Häggkvist conjecture
Every digraph on $n$ vertices with minimum out-degree $\ge n / r$ has a directed cycle of length $\le r$.
Rainbow generalization
Let $G$ be an edge-colored graph on $n$ vertices. If there are $n$ color classes, each of size $\ge n/r$, then $G$ has a rainbow cycle of length $\le r$.
Common theme
Given edge sets $E_1, \dots, E_m$, find a rainbow set $E$ consists of at most $1$ edge from each $E_i$.
Rainbow matching
Given macthings $E_1, \dots, E_m$,
a rainbow matching $E$ is a matching and a rainbow set
Pokrovskiy: $n$ matchings of size $n+o(n)$ in a bipartite graph have a rainbow matching of size $n$.
Woolbright: $n$ matchings of size $n$ in a bipartite graph have a rainbow matching of size $n - \sqrt{n}$.
Question: ? matchings of size $n$ in a bipartite graph have a rainbow matching of size $n$.
$(n-1)$ x red matching of size $n$ + $(n-1)$ x blue matching of size $n$
Answer: $2n-1$ matchings of size $n$ in a bipartite graph have a rainbow matching of size $n$.
Drisko: $2n-1$ perfect matchings of size $n$ in a bipartite graph have a rainbow perfect matching.
Plan of talk
Geometric proof of Drisko
Topological toolkit
Applications
Bárány's Colorful Carathéodory
If $x \in \mathbb{R}^d$ lies in $\mathrm{conv}(P_k)$ for $k=1,2, \dots, d+1$ then $x$ lies in the convex hull of a rainbow set.
Cone version
If $x \in \mathbb{R}^d$ lies in $\mathrm{pos}(P_k)$ for $k=1,2,\dots,d$ then $x$ lies in the positive cone of a rainbow set.
Drisko: $2n-1$ perfect matchings of size $n$ in a bipartite graph have a rainbow perfect matching.
Standard basis of $\mathbb{R}^{2n}$: $u_1, \dots, u_n$, $v_1, \dots, v_n$
edge $u_i \sim v_j$ $\Leftrightarrow$ $u_i + v_j \in \mathbb{R}^{2n}$
edge set $E_k$ $\Leftrightarrow$ $P_k := \big\{u_i + v_j : u_i\sim v_j \text{ in }E_k\big\}$
$E_k$ is perfect matching $\Leftarrow$$\Rightarrow$ $\vec{1} := \sum u_i + \sum v_i \in \mathrm{pos}(P_k)$
Fix: $P_k$ and $\vec{1}$ live in a 1-codimensional subspace of $\mathbb{R}^{2n}$
Bárány: $\vec{1}$ is in the cone of a rainbow set $x_1 \in P_1, \dots, x_{2n-1}\in P_{2n-1}$
$\Rightarrow$ a rainbow perfect matching
Aharoni–Berger
$2n-1$ matchings of size $n$ in a bipartite graph have a rainbow matching of size $n$.
Standard basis of $\mathbb{R}^{?}$: $u_1, u_2, \dots$, $v_1, v_2, \dots$
No control on dimension of ambient space
Plan of talk
Geometric proof of Drisko
Topological toolkit
Applications
Simplicial complex $\mathcal{C}$ is a family of sets such that $\sigma \subseteq \tau, \tau \in \mathcal{C} \implies \sigma\in \mathcal{C}$.
$V = \{1,2,3,4\}$, $\mathcal{C} = \{\emptyset, \{1\}, \{2\}, \{3\}, \{4\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}, \{3,4\}\}$
Kalai–Meshulam
Let $V_1, \dots, V_{d+1} \subset V$. If $\mathcal{C}$ is a $d$-Leray simplicial complex on $V$ and no $V_k$ is in $\mathcal{C}$, then a rainbow set is not in $\mathcal{C}$.
"Definition" $\mathcal{C}$ is $d$-Leray if $\mathcal{C}$ does not have "holes" of dimension $\ge d$.
Kalai–Meshulam
Let $V_1, \dots, V_{d+1} \subset V$. If $\mathcal{C}$ is a $d$-Leray simplicial complex on $V$ and no $V_k$ is in $\mathcal{C}$, then a rainbow set is not in $\mathcal{C}$.
Bárány
If $x \in \mathbb{R}^d$ lies in $\mathrm{conv}(P_k)$ for $k=1,2, \dots, d+1$ then $x$ lies in the convex hull of a rainbow set.
Proof sketch (Kalai–Meshulam $\implies$ Bárány)
Construct $\mathcal{C}$ on $V$ such that $x\in \mathrm{conv}(P_k) \Leftrightarrow V_k \not\in \mathcal{C}$
Kalai–Meshulam: if $\mathcal{C}$ is $d$-Leray then a rainbow set $\not\in\mathcal{C}$
$\Rightarrow$ $x \in \mathrm{conv}($a rainbow set$)$.
How to prove $\mathcal{C}$ is $d$-Leray?
Wegner
| $d$-representable Bárány geometric | $\subset$ | $d$-collapsible $\Leftarrow$ combinatorial | $\subset$ | $d$-Leray Kalai–Meshulam topological |
Elementary $d$-collapse
1. Pick $\sigma \in \mathcal{C}$ such that $|\sigma|\le d$
2. If max face $\tau \supseteq \sigma$ is unique then remove $[\sigma, \tau]$
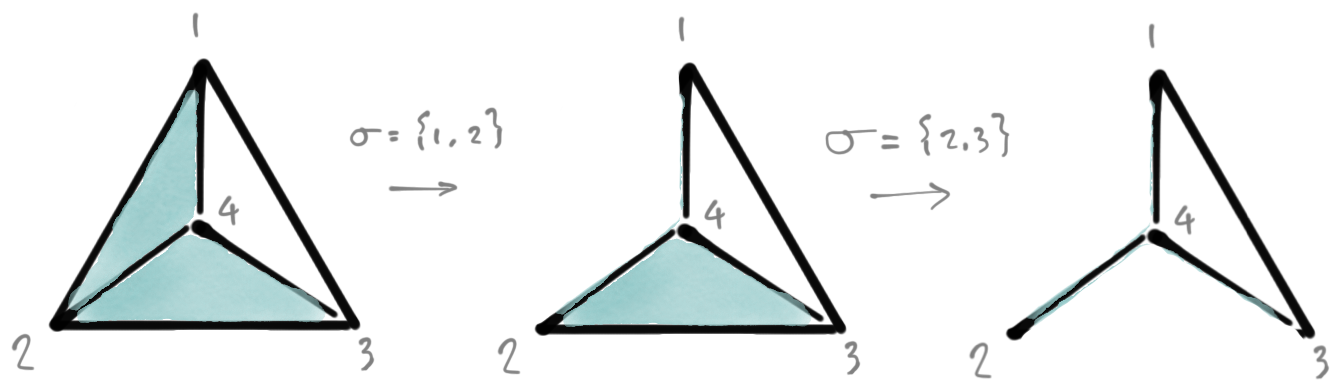
$\mathcal{C}$ is $d$-collapsible if a chain of elementary $d$-collapses would turn $\mathcal{C}$ into $\{\emptyset\}$
Plan of talk
Geometric proof of Drisko
Topological toolkit
Applications
Kalai–Meshulam
Let $V_1, \dots, V_{d+1} \subset V$. If $\mathcal{C}$ is a $d$-collapsible simplicial complex on $V$ and no $V_k$ is in $\mathcal{C}$, then a rainbow set is not in $\mathcal{C}$.
Aharoni–Berger
$2n-1$ matchings of size $n$ in a bipartite graph have a rainbow matching of size $n$.
Proof sketch (Kalai–Meshulam $\implies$ Aharoni–Berger)
$V := E_1 \cup \dots \cup E_{2n-1}$, $\mathcal{C} := \{ E\subset V : \nu(E) < n \}$
$\nu(E)$ is the matching number of $E$
Kalai–Meshulam: If $\mathcal{C}$ is $(2n-2)$-collapsible then a rainbow set is not in $\mathcal{C}$
$\Rightarrow$ a rainbow mathching of size $\ge n$.
Business model
- Pick your favorite graph parameter $\nu$
- Prove $\mathcal{C} := \{ E : \nu(E) < n\}$ is $d$-collapsible
- Apply Kalai–Meshulam
Rainbow result: Edge sets $E_1, \dots, E_{d+1}$ with $\nu(E_k) \ge n$ have a rainbow set $E$ with $\nu(E) \ge n$.
Aharoni, Holzman, J.
Given $r\in\mathbb{N}$, $n\in\mathbb{N}$ and $r$-partite edge sets $E_1, \dots, E_{rn-r+1}$ with $\nu^*(E_i) \ge n$ there is a rainbow set $E$ with $\nu^*(E) \ge n$.
Here the fractional matching number $\nu^*(E) = \max_f\sum_{e\in E} f(e)$
s.t. $f(e)\ge 0$ for $e\in E$ and $\sum_{e\ni v} f(e) \le 1$ for $v\in V$.
Easter egg
Drisko's theorem
$2n-1$ perfect matchings of size $n$ in a bipartite graph have a rainbow perfect matching.
Erdős–Ginzburg–Ziv
Given $2n-1$ numbers in $\mathbb{Z}/n \mathbb{Z}$, there exist $n$ of them that sum to $0$.
Alon's proof (Drisko $\implies$ Erdős–Ginzburg–Ziv)
For each number $a_i$, let $E_i$ be matching $\{ x \sim x + a_i\}$
Drisko: there is a rainbow matching of size $n$
$1 \sim 1 + a_{i_1}, \dots, n \sim n + a_{i_n}$
Rainbow means $i_1, \dots, i_n$ are different
$\implies 1 + \dots + n = (1 + a_{i_1}) + \dots + (n + a_{i_n})$
An open problem
3 x blue+ 3 x red+ 1 x green
no rainbow matching of size $4$
Conjecture
$2n$ matchings of size $n$ in any graph have a rainbow matching of size $n$.
Aharoni, Berger, Chudnovsky, Howard, Seymour
$3n-2$ matchings of size $n$ have a rainbow matching of size $n$.
Massachusetts Institute of Technology
zilinj@mit.edu