Negligible obstructions and Turán exponents
姜子麟 Zilin Jiang
Joint work with 江滔 Tao Jiang and 马杰 Jie Ma
Turán number
$\mathrm{ex}(n ,F) = $ max number of edges in $n$-vertex graph, contains no $F$ (forbidden subgraph) as subgraph
Rational exponents conjecture
$\forall$ bipartite $F$ $\exists r \in \mathbb{Q}$ s.t. $\mathrm{ex}(n, F) = \Theta(n^r)$.
At present these conjectures which are about 20 years old are beyond our reach. – Erdős 1988
Realizability conjecture
$\forall r \in \mathbb{Q} \cap (1,2)$ $\exists$ bipartite $F$ s.t. $\mathrm{ex}(n, F) = \Theta(n^r)$.
Realizability conjecture
$\forall r \in \mathbb{Q} \cap (1,2)$ $\exists$ bipartite $F$ s.t. $\mathrm{ex}(n, F) = \Theta(n^r)$.
Bukh and Conlon 2015 breakthrough
$\forall r \in \mathbb{Q} \cap (1,2)$ $\exists$ finite family $\mathcal{F}$ s.t. $\mathrm{ex}(n, \mathcal{F}) = \Theta(n^r)$.
Rooted graph $F$ is graph $F$ equipped with $R(F) \subset V(F)$.
$p$-th power of $F$ is $p$ disjoint copies of $F$ identified at roots.
Bukh–Conlon conjecture
$\forall$ balanced rooted tree $F$ and $p$, $\mathrm{ex}(n, F^p) = O(n^{2-1/\rho_F})$.
Intermediate conjecture
$\forall$ rational $\rho > 1$ $\exists$ balanced rooted tree $F$ with density $\rho$ s.t. $\mathrm{ex}(n, F^p) = O(n^{2-1/\rho})$ for every $p$.
Bukh and Conlon
- $\forall$ balanced rooted tree $F$ $\exists$ p, $\mathrm{ex}(n, F^p) = \Omega(n^{2-1/\rho_F})$.
- $\forall$ $\rho > 1$ $\exists$ balanced rooted tree $F$ with density $\rho$.
Realizability conjecture
$\forall r \in \mathbb{Q} \cap (1,2)$ $\exists$ bipartite $F$ s.t. $\mathrm{ex}(n, F) = \Theta(n^r)$.
Intermediate conjecture
$\forall \rho \in \mathbb{Q}$ with $\rho > 1$ $\exists$ balanced rooted tree $F$ with density $\rho$ s.t. $\mathrm{ex}(n, F^p) = O(n^{2-1/\rho})$ for every $p$.
Kővári, Sós, Turán 1954, Faudree, Simonovits 1983
Jiang, Ma, Yepremyan, Kang, Kim, Liu, Conlon, Janzer, Lee, Qiu

Jiang, J. and Ma 2020
New densities $\rho$, for example:
$m + 5/8, m + 7/10$ for $m \ge 2$.
Thought experiment
$F$ is a rooted tree and $G$ is a $d$-regular $n$-vertex graph.
Task: when $d = \omega(n^{1-1/\rho_F})$, try to find $F^p$ in $G$.
An embedding $\eta$ from $F$ to $G$ is an injection $\eta\colon V(F) \to V(G)$ s.t. $\{u_1, u_2\} \in E(F) \implies \{\eta(u_1), \eta(u_2)\} \in E(G)$.
Observation 1: $\# \{F \hookrightarrow G\} = \Omega(nd^{e(F)}) = \omega(n^{\lvert{R(F)}\rvert})$.
Observation 2: $\exists \sigma\colon R(F) \to V(G)$ s.t. $\# \{F \hookrightarrow G \mid \sigma\} = \omega(1)$,
where $\{F \hookrightarrow G \mid \sigma\}$ consists of embeddings from $F$ to $G$
that agree with $\sigma$ on the roots of $F$.
For example, $F$ is.
Ideally, images of non-roots of $F$ are pairwise disjoint, but perhaps...
An embedding $\eta$ from $F$ to $G$ is $C$-ample if $\exists \eta_1, \dots, \eta_C$ s.t.
they agree with $\eta$ on $R(F)$, but images of non-roots are pairwise disjoint.
- Ideal scenario: $\exists$ $\omega(1)$-ample embedding from $F$ to $G$
- Undesirable scenarios: $\exists$ $\omega(1)$-ample embedding from $F_0$ to $G$ for some subtree $F_0$ of $F$
How to characterize the undesirable scenarios?
A family $\mathcal{F}_0$ of subtrees (each with more than $1$ edges) of $F$ is an obstruction family for $F$ if after converting any (proper) subset of non-roots to roots in $F$, the resulting rooted graph contains a member of $\mathcal{F}_0$ as a rooted subgraph ($F_0 \subseteq F$ and $R(F_0) \subseteq R(F)$).
For example, $F$ is, and
$\mathcal{F}_0 = \{$,$\}$ is an obstruction family for $F$.
How to resolve the undesirable scenarios?
Given $F_0 \in \mathcal{F}_0$ and $F$, $F_0$ is negligible for $F$ if for every $p \in \mathbb{N}^+, \epsilon > 0$ $\exists c_0 > 0, M \in \mathbb{N}$ s.t. $\forall c > c_0$ and $n$-vertex graph $G$, if degrees of $G$ are between $d$ and $5^{4/\alpha}d$, where $\alpha = 1-1/\rho_F$ and $d = cn^\alpha$, and $\{F \hookrightarrow_p G\} = \emptyset$ then $\#\{F_0 \hookrightarrow_M G\} < (\epsilon + o(1))nd^{e(F_0)}$.
"The undesirable scenarios rarely happen."
Negligibility lemma
Given $\mathcal{F}_0$, if every member of $\mathcal{F}_0$ is negligible for $F$, then $\mathrm{ex}(n, F^p) = O(n^{2-1/\rho_F})$ for every $p$.
Strategy: 1. Identify an obstruction family; 2. Certify its negligibility.
Application

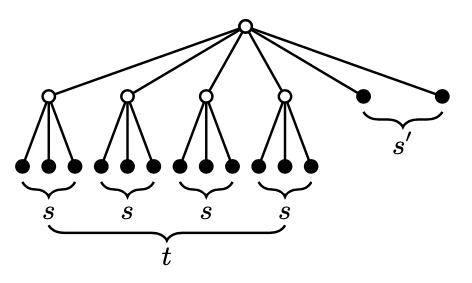
Obstruction family $\mathcal{F}_0$ for $F_{s,t,s'}$ is
$\{ K_{1, s+1} \} \cup \{ F_{s,t-i,s'+i} \colon 1 \le i \le s-s' \}$
Fact: $F_{s,t,s'}$ is balanced $\Leftrightarrow - 1 \le s - s' \le t$ and $(t, s') \neq (1,0)$.
Negligibility for $F_{s,t,s'}$ with a technical condition
If $F_{s,t,s'}$ is balanced and $t \ge s^3 - 1$, then $\mathcal{F}_0$ is negligible for $F_{s,t,s'}$.
Conjecture (negligibility for $F_{s,t,s'}$)
If $F_{s,t,s'}$ is balanced, then $\mathcal{F}_0$ is negligible for $F_{s,t,s'}$.
For every $s < a$, would give new densities $m + s/a$ for all $m \ge m_0(s,a)$.