Turán number

$\mathrm{ex}(n ,F) = $ max number of edges in $n$-vertex graph, contains no $F$ (forbidden subgraph) as subgraph

At present these conjectures which are about 20 years old are beyond our reach. – Erdős 1988

Rooted graph $F$ is graph $F$ equipped with $R(F) \subset V(F)$.

$p$-th power of $F$ is $p$ disjoint copies of $F$ identified at roots.

Thought experiment

$F$ is a rooted tree and $G$ is a $d$-regular $n$-vertex graph.
Task: when $d = \omega(n^{1-1/\rho_F})$, try to find $F^p$ in $G$.

An embedding $\eta$ from $F$ to $G$ is an injection $\eta\colon V(F) \to V(G)$ s.t. $\{u_1, u_2\} \in E(F) \implies \{\eta(u_1), \eta(u_2)\} \in E(G)$.

Observation 1: $\# \{F \hookrightarrow G\} = \Omega(nd^{e(F)}) = \omega(n^{\lvert{R(F)}\rvert})$.

Observation 2: $\exists \sigma\colon R(F) \to V(G)$ s.t. $\# \{F \hookrightarrow G \mid \sigma\} = \omega(1)$,
where $\{F \hookrightarrow G \mid \sigma\}$ consists of embeddings from $F$ to $G$
that agree with $\sigma$ on the roots of $F$.

For example, $F$ is.

Ideally, images of non-roots of $F$ are pairwise disjoint, but perhaps...

An embedding $\eta$ from $F$ to $G$ is $C$-ample if $\exists \eta_1, \dots, \eta_C$ s.t.
they agree with $\eta$ on $R(F)$, but images of non-roots are pairwise disjoint.

• Ideal scenario: $\exists$ $\omega(1)$-ample embedding from $F$ to $G$
• Undesirable scenarios: $\exists$ $\omega(1)$-ample embedding from $F_0$ to $G$ for some subtree $F_0$ of $F$

How to characterize the undesirable scenarios?

A family $\mathcal{F}_0$ of subtrees (each with more than $1$ edges) of $F$ is an obstruction family for $F$ if after converting any (proper) subset of non-roots to roots in $F$, the resulting rooted graph contains a member of $\mathcal{F}_0$ as a rooted subgraph ($F_0 \subseteq F$ and $R(F_0) \subseteq R(F)$).

For example, $F$ is, and
$\mathcal{F}_0 = \{$,$\}$ is an obstruction family for $F$.

How to resolve the undesirable scenarios?

Given $F_0 \in \mathcal{F}_0$ and $F$, $F_0$ is negligible for $F$ if for every $p \in \mathbb{N}^+, \epsilon > 0$ $\exists c_0 > 0, M \in \mathbb{N}$ s.t. $\forall c > c_0$ and $n$-vertex graph $G$, if degrees of $G$ are between $d$ and $5^{4/\alpha}d$, where $\alpha = 1-1/\rho_F$ and $d = cn^\alpha$, and $\{F \hookrightarrow_p G\} = \emptyset$ then $\#\{F_0 \hookrightarrow_M G\} < (\epsilon + o(1))nd^{e(F_0)}$.

"The undesirable scenarios rarely happen."

Strategy: 1. Identify an obstruction family; 2. Certify its negligibility.

Application

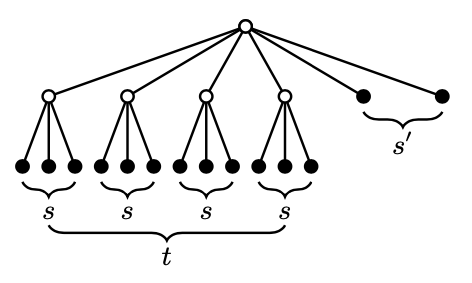
Obstruction family $\mathcal{F}_0$ for $F_{s,t,s'}$ is
$\{ K_{1, s+1} \} \cup \{ F_{s,t-i,s'+i} \colon 1 \le i \le s-s' \}$

Fact: $F_{s,t,s'}$ is balanced $\Leftrightarrow - 1 \le s - s' \le t$ and $(t, s') \neq (1,0)$.

For every $s < a$, would give new densities $m + s/a$ for all $m \ge m_0(s,a)$.