Eigenvalues, Forbidden Subgraphs and Ramsey
姜子麟 Zilin Jiang
Arizona State University
June 16, 2022
Joint work with Саша Полянский Alexandr Polyanskii
Part I
Eigenvalues
Adjacency matrix and smallest eigenvalue
| $G$ | $\lambda_1(G)$ |
| $K_n$ | $-1$ |
| $K_{1,n}$ | $-\sqrt{n}$ |
| $P_n$ | $-2\cos\frac{\pi}{n+1}$ |
$\lim_n \lambda_1(P_n) = -2$
What's the limit of the smallest eigenvalue? $-\lambda^*$
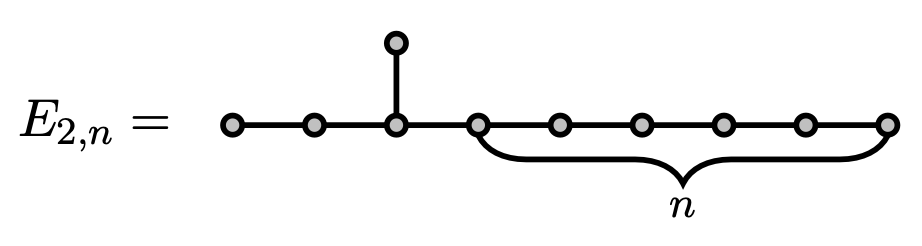
$\lambda^* = \sqrt{\beta}+1/\sqrt{\beta} = $ 2.019800887...
where $\beta$ is real root of $x^3 = x + 1$.
Characterization of graphs with bounded eigenvalues
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
Cauchy interlacing theorem
$\mathcal{G}(\lambda)$ is closed under taking subgraphs
* all subgraphs are induced
Part II
Forbidden subgraphs
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
$\mathcal{G}(\lambda)$ is closed under taking subgraphs
Planar graphs are closed under taking minors
Wagner's theorem: no $K_5$ or $K_{3,3}$ minors
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
$\mathcal{G}(\lambda)$ is closed under taking subgraphs
Question: Define $\mathcal{G}(\lambda)$ by forbidden subgraphs?
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
Question: Define $\mathcal{G}(\lambda)$ by forbidden subgraphs?
Simple case $\lambda < 1$
$\lambda_1(K_2) = -1$ hence $K_2 \not\in \mathcal{G}(\lambda)$
$\mathcal{G}(\lambda) = \{$ graphs with no edges $\}$
Tautology: Forbid all graphs outside $\mathcal{G}(\lambda)$
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
Question [Bussemaker and Neumaier 1992]
Can $\mathcal{G}(\lambda)$ be defined by finite forbidden subgraphs?
$\mathcal{G}(2)$ is complex; it contains all the line graphs
Cameron, Goethals, Seidel, and Shult: For every connected graph, it is in $\mathcal{G}(2)$ if and only if it is represented by a subset of $D_n$ or $E_8$ (root systems).
Kumar, Rao and Singhi $\mathcal{G}(2)$ can be defined by forbidden subgraphs with $\le 10$ vertices
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
Can $\mathcal{G}(\lambda)$ be defined by finite forbidden subgraphs?


J. and Polyanskii 2022+
Yes if and only if $\lambda < \lambda^* \approx 2.01980$
Generalization to signed graphs
$\mathcal{G}^\pm(\lambda) = \{$ signed graphs with smallest e.v. $\ge -\lambda\}$
Can $\mathcal{G}^\pm(\lambda)$ be defined by finite forbidden subgraphs?
J. and Polyanskii 2022+ Yes if and only if $\lambda < \lambda^*$
Motivation [Tidor, Yao, Zhang and Zhao 2022] Application to spherical two distance sets
Another application
For every $λ < λ^*$, there exists $n$ s.t. for every symmetric integer matrix $A$ whose diagonal entries are all zero, if $A$ has an eigenvalue less than $-λ$, then so does one of its principal submatrix of order at most $n$. The same conclusion does not hold for any $λ ≥ λ^*$
Vijayakumar: for $λ = 2$ the natural number $n$ can be as small as (but no smaller than) $10$.
Part III
Ramsey
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
$\mathcal{G}(\lambda)$ can be defined by finite forbidden subgraphs
if and only if $\lambda < \lambda^* \approx 2.01980$
Break into three cases
$\lambda < 2$
$2 \le \lambda < \lambda^*$
$\lambda \ge \lambda^*$
Case 1: For $\lambda < 2$, $\mathcal{G}(\lambda)$ can be defined by finite forbidden subgraphs
Ramsey-type result
For every $F$ and $\ell, m$ there exists $N$ s.t. for every connected graph $G$ with more than $N$ vertices, if no member in $\{K_{1,4}\} \cup \mathcal{X}(F, \ell, m)$ is a subgraph of $G$ then $F$ is not a subgraph of $G$.
Here, the extension family $\mathcal{X}(F, \ell, m)$ consists of

Step 1: Find $\ell, m$ such that both $\mathcal{X}(C, \ell, m)$ and $\mathcal{X}(D, \ell, m)$ are disjoint from $\mathcal{G}(\lambda)$
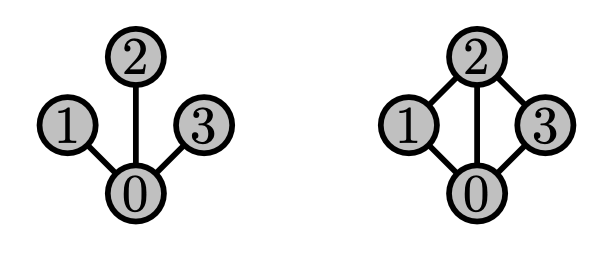
Forbid $\{K_{1,4}\} \cup \mathcal{X}(C, \ell, m) \cup \mathcal{X}(D, \ell, m)$
Fact (van Rooij and Wilf): Every graph that contains neither $C$ nor $D$ as a subgraph is a line graph
What're left to forbid?
Graphs with at most $N$ vertices and line graphs
Step 2: Forbid graphs outside $\mathcal{G}(\lambda)$ with at most $N$ vertices, $P_\ell$, some path-clique/clique extensions of cycles, and some clique extensions of cliques
What're still left to forbid?
Line graphs of rooted trees $T$, where $T$ is of depth $\le \ell$, and all vertices but root of $T$ have degree $\le m$
Step 3: Forbid $L(T)$ for $T$ that is minimal in $\mathcal{F}$, where $\mathcal{F} = \{T \colon L(T) \not\in \mathcal{G}(\lambda)$ depth of $T \le \ell$ and degrees of non-roots are $\le m\}$
Are there only finitely many minimal $T$ in $\mathcal{F}$?
Step 3.1: Enumerate bounded trees $T_1, T_2, \dots, T_n$
Step 3.2: Encode each $T \in \mathcal{F}$ by $(t_1, \dots, t_n)$ where $t_i$ is the # of occurrences of $T_i$ as a connected component in the graph obtained by removing the root from $T$.
Encodings of minimal $T$ form an antichain in $(\mathbb{N}^n, ≤)$
Step 3: Forbid $L(T)$ for $T$ that is minimal in $\mathcal{F}$, where $\mathcal{F} = \{T \colon L(T) \not\in \mathcal{G}(\lambda)$ depth of $T \le \ell$ and degrees of non-roots are $\le m\}$
Are there only finitely many minimal $T$ in $\mathcal{F}$?
Encodings of minimal $T$ form an antichain in $(\mathbb{N}^n, ≤)$
Dickson's lemma
The poset $(\mathbb{N}^n, ≤)$ does not contain infinite antichains
Case 2: For $2 \le \lambda < \lambda^*$, $G(\lambda)$ can be defined by finite forbidden subgraphs
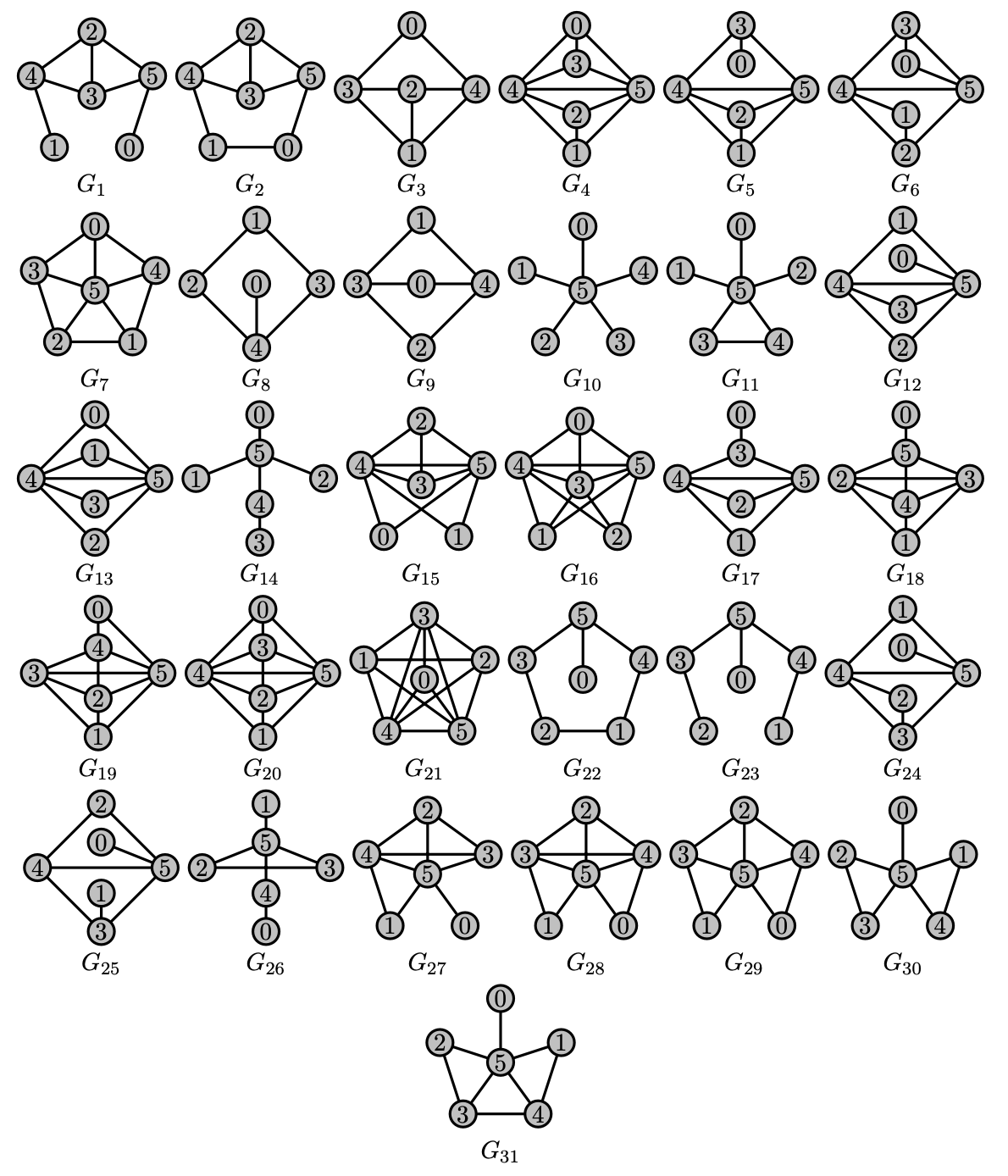
- Similar Ramsey-type argument
- Use graphs on right in place of $C$ and $D$
- Computer assisted proof
- $G_{23}$ is critical
Open problems
Problem A: Effectivization
Problem B: Classify all the connected graphs with smallest eigenvalue in $(-λ^*,-2)$. In particular, classify those that have sufficiently many vertices.
Problem C: Same problem but for signed graphs
Problem D:Forbidden principle submatrices for $\{-1,0,+1\}$-valued symmetric matrices with eigenvalues bounded from below; connection to Lehmer's Mahler measure problem
Arizona State University
zilinj@asu.edu