Beyond the classification theorem of
Cameron, Goethals, Seidel and Shult
Zilin Jiang
Arizona State University
Joint work with Hricha Acharya

Hricha Acharya
$-\lambda^* = -2.0198008871...$
$-\lambda^* = -2.0198008871...$
the limit of the smallest eigenvalue of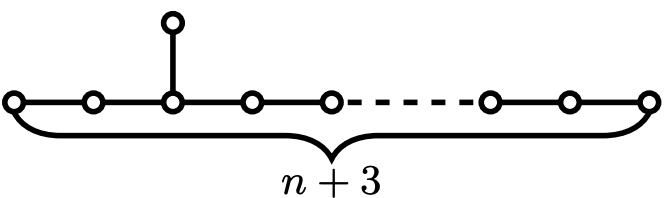
(refer to adjacency matrices)
Fundamental problem
Classification and characterization of graphs with bounded eigenvalues
$\mathcal{G}(\lambda) = \{$ graphs with smallest eigenvalue $\ge -\lambda \}$
$\mathcal{G}(2) = \{$ graphs with smallest eigenvalue $\ge -2 \}$
Outline
- History of $\mathcal{G}(2)$
- Classify $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
- Beyond $\mathcal{G}(\lambda^*)$
History of $\mathcal{G}(2)$
$\mathcal{G}(2) = \{$graphs with smallest eigenvalue $\ge -2 \}$
$\mathcal{G}(2) \supset \{$line graphs$\}$
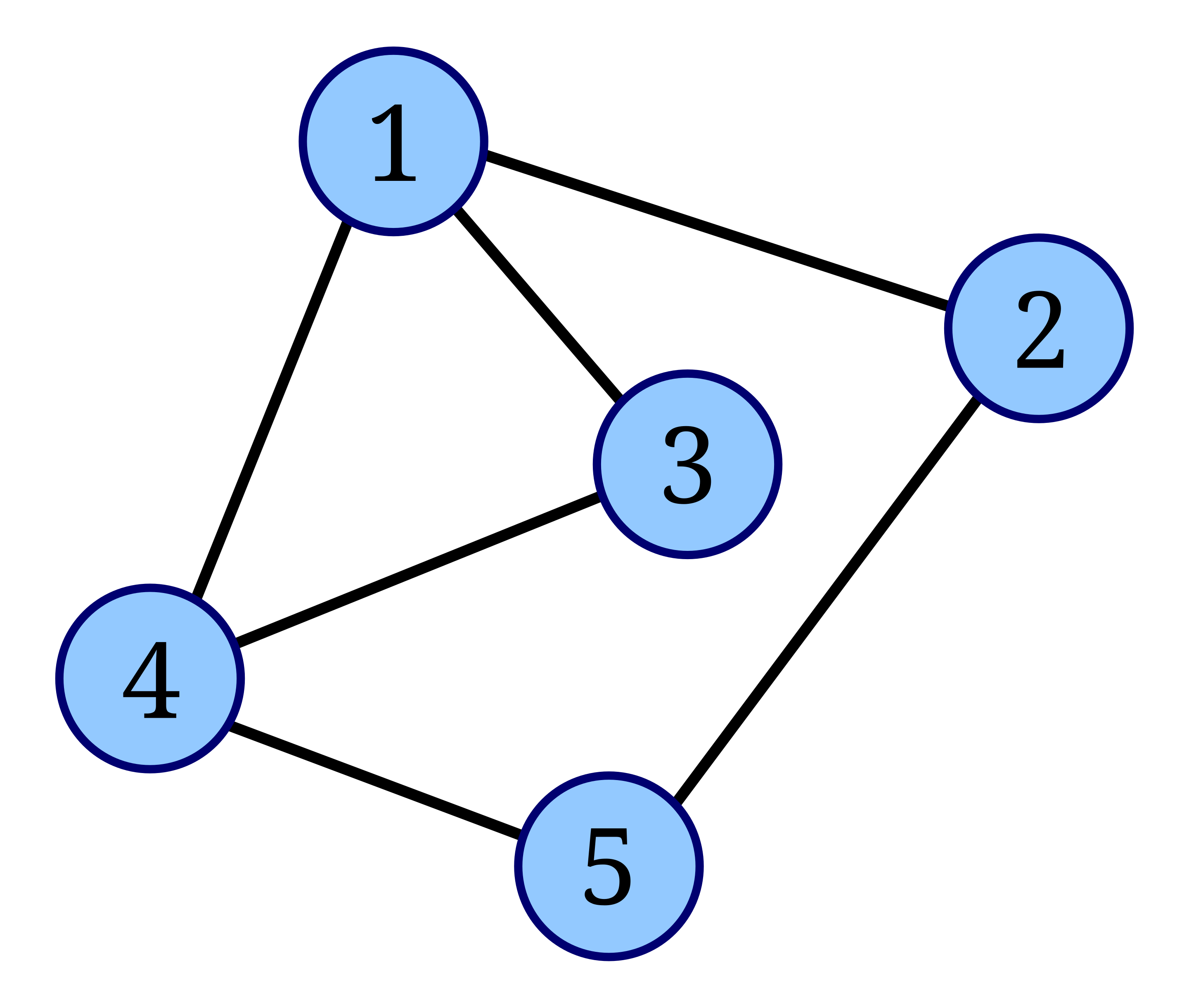
incidence matrix $B$

$A = B^\intercal B - 2I$
$\mathcal{G}(2) \supset \{$line graphs$\}$
Hoffman · 1969 $\mathcal{G}(2) \supset \{$generalized line graphs$\}$
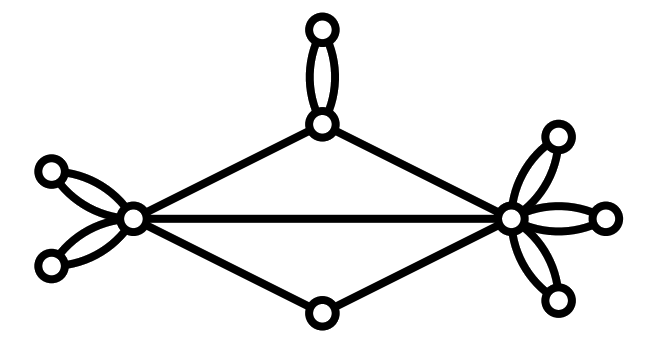
graph with "petals"
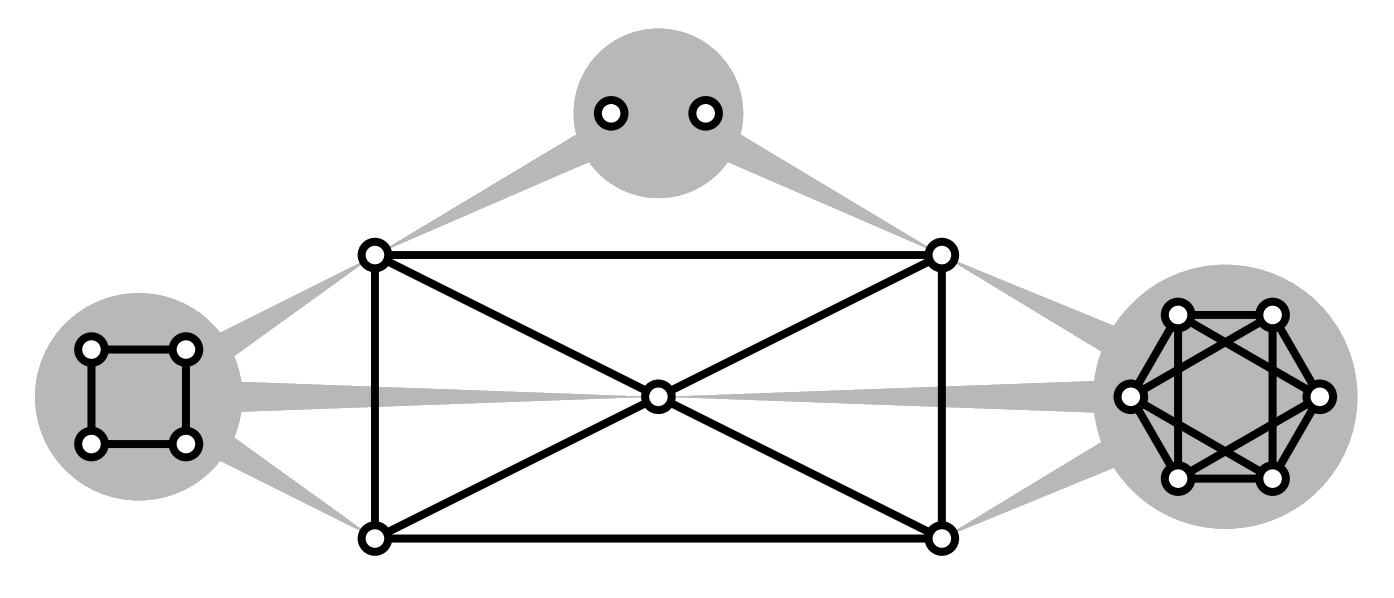
edges share exactly one vertex
Hoffman · 1969 $\mathcal{G}(2) \supset \{$generalized line graphs$\}$
Observation If $G \in \mathcal{G}(2)$, then components $\in \mathcal{G}(2)$
Cameron, Goethals, Seidel, and Shult · 1976
- $\{$connected $\mathcal{G}(2)\} \setminus \{$connected generalized line graphs$\} = \{$exceptional graphs$\}$
- each is represented by subset of $E_8$ root system
- each has at most $36$ vertices
Outline
- History of $\mathcal{G}(2)$
- Classify $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
- Beyond $\mathcal{G}(\lambda^*)$
Classify $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
But 😕 why $\lambda^*$?
J. and Polyanskii $\mathcal{G}(\lambda) \setminus \mathcal{G}(2)$ is finite for $\lambda < \lambda^*$
*Only consider connected graphs from now on
Observation $\{$ $\} \subset \mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
$\} \subset \mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
$\lambda^*$ is smallest s.t. $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ is infinite 🙂
J. and Acharya
Complete classification of $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
Low-res version
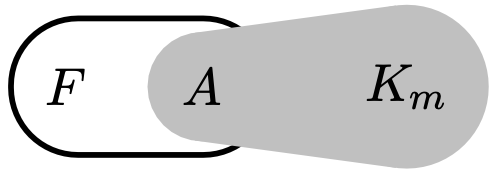
Every big graph in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ looks like
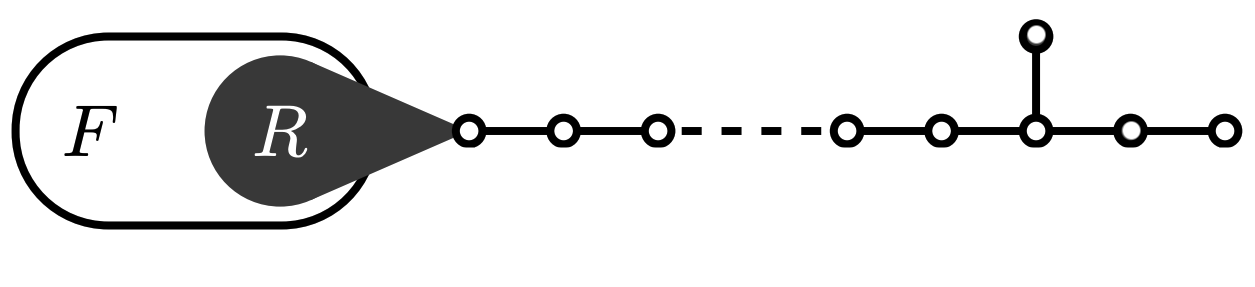
augmented path extension (ape)
Low-res version
Every big graph in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ looks like

augmented path extension (ape)
| Questions | Answers |
| Classify $F_R$? | 794, at most 14 vertices |
| Describe $\ell$? | For $F_R$, $\ell \ge \ell_0$ |
| Enumerate non-apes? | 4752 mavericks at most 19 vertices |
Outline
- History of $\mathcal{G}(2)$
- Classify $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$
- Beyond $\mathcal{G}(\lambda^*)$
A notable portion of mavericks look alike
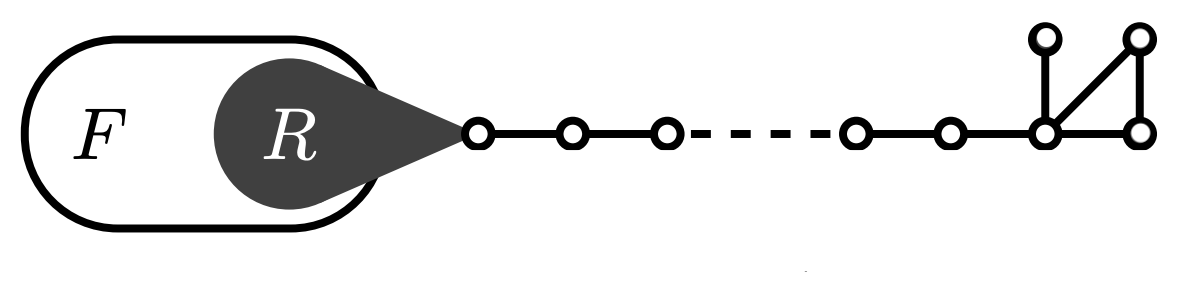
$-\lambda^{**} = -2.02124$
the limit of the smallest eigenvalue of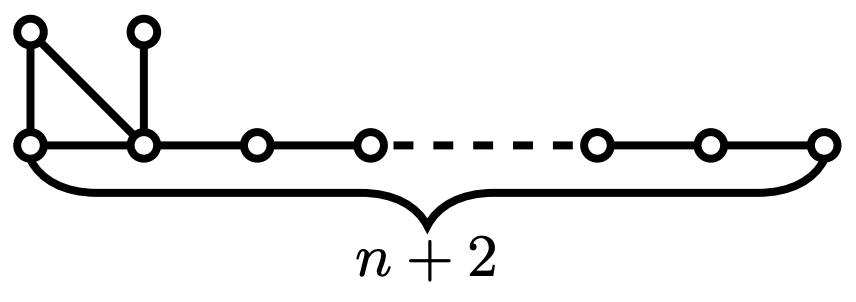
Low-res version
For $\lambda \in (\lambda^*, \lambda^{**})$,
eEvery big graph in $\mathcal{G}(\lambda$$^*$$) \setminus \mathcal{G}(2)$ looks like
Observation $\{$ $\} \subset \mathcal{G}(\lambda^{**}) \setminus \mathcal{G}(2)$
$\} \subset \mathcal{G}(\lambda^{**}) \setminus \mathcal{G}(2)$
Low-res version
For $\lambda \in (\lambda^*, \lambda^{**})$,
every big graph in $\mathcal{G}(\lambda) \setminus \mathcal{G}(2)$ looks like
| Question | Answer |
| Classify $F_R$? | Infinite |
Proof techniques
Low-res version
Every big graph in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ looks like
Weaker version
Every big graph in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ contains
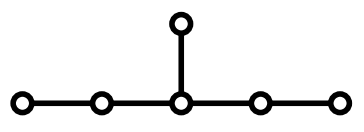
Weaker version
Every big graph in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ contains

Cvetković, Doob, and Simić · 1981
Rao, Singhi, and Vijayan · 1981
If $G$ is not a generalized line graph, then $G$ contains ...
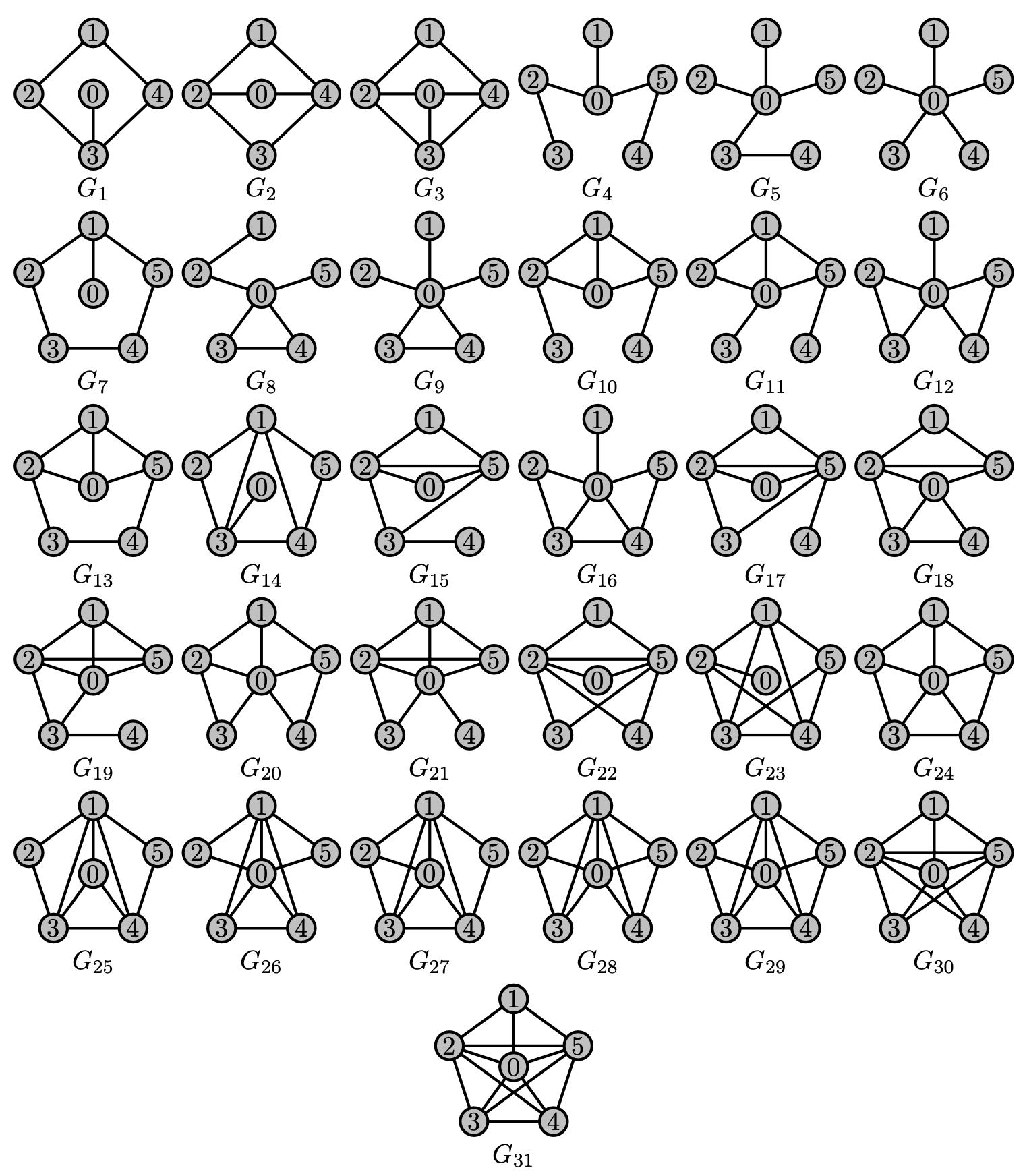
Suffices to show
Every big graph in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ contains no $F$ in

Assume that big $G$ in $\mathcal{G}(\lambda^*) \setminus \mathcal{G}(2)$ contains $F$
Ramsey theorem for connected graphs
If big $G$ contains $F$, then $G$ contains
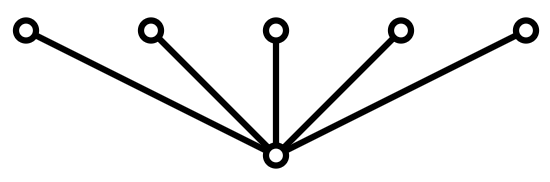

Observation  $\not\in \mathcal{G}(\lambda^*)$
$\not\in \mathcal{G}(\lambda^*)$
Lemma If  $\not\in \mathcal{G}(\lambda^*)$, then the same holds for
$\not\in \mathcal{G}(\lambda^*)$, then the same holds for 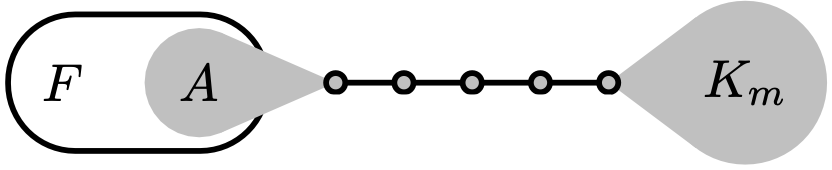
Check  $\not\in \mathcal{G}(\lambda^*)$ for $F$ in
$\not\in \mathcal{G}(\lambda^*)$ for $F$ in

Open problems
Problem A Classify graphs with smallest eigenvalues in $(-\lambda^{**},-\lambda^*)$.
Problem B Classify signed graphs with smallest eigenvalue in $(-\lambda^*,-2)$.
Signed graphs are graphs with edges labeled by $+$ or $-$
Refer to signed adjacency matrix
In particular, classify those that are big.